An element of P(2) can be expressed as a composite of
at most three maps obtained from perspectivities. Lemma 2
For λ ≠ 0, there exist perspectivities which correspond
to the following elements of P(2):
u([x,y,z]) = [x/λ,y,z],
v(x,y,z) = [x,y/λ,z], and
w(x,y,z) = [x,y,z/λ].
Proof
We consider just the third, the others are similar.
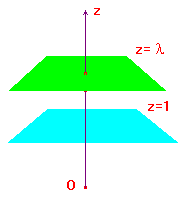
The perspectivity w from z=1 to z=λ with vertex O
as a map of R3 maps D(x,y,1) to D'(λx,λy,λ).
We must now reposition the plane at z=λ to the
position z=1 by projection parallel to the z-axis.
Then D' moves to (λx,λy,1). The result follows as
[λx,λy,1] = [x,y,1/λ], so we get the correct effect
as a transformation of RP2.
Suppose that t is the element of P(2) which maps [x] to [Ax].
We will show that t can be built from perspectivities.
We know that an element of P(2) is determined by the images of
four p-points, no three of which are collinear. We usually choose
X = [1,0,0], Y = [0,1,0], Z = [0,0,1] and U = [1,1,1], but here it
is easier to work in reverse.
Let P = t-1(X), Q = t-1(Y),
R = t-1(Z), S = t-1(U).
These p-points are four lines through O, with no three coplanar.
We can choose a plane Π not through O, and not parallel to any
of these lines, so each line meets Π. Let these intersections be
the points P, Q, R and S, respectively.
Now position this plane in R3 so P,Q,R lie on the x-, y- and z-axes
respectively
This can be done as P,Q,R are non-collinear.
Let Π' be the plane x+y+z=1 - the plane containing the points
X(1,0,0), Y(0,1,0) and Z(0,0,1), on X, Y and Z,
respectively.
Let a be the perspectivity from Π to Π' with vertex O. Then a
maps P, Q and R to X, Y and Z, respectively. Suppose that it
maps S to W = (k,l,m). Since S is not collinear with any two of
P, Q and R, W is not collinear with any two of X, Y and Z, so
that k,l,m are non-zero.
From Lemma 2, we have perspectivities:
b(x,y,z) = ((m/k)x,y,z), and
c(x,y,z) = (x,(m/l)y,z).
We observe that [m,m,m] = [1,1,1] = U.
Then coboa maps P, Q, R and S
to X, Y, Z and U, i.e. has
the same effect as t on these four p-points, and hence
on all of RP2