definition
A subset S of the disk D is convex if, for A,BεS,
the segment AB lies in S
In hyperbolic geometry, this means that the entire hyperbolic segment AB is in S.
Note that
hyperbolic transformations map segments to segments, so convexity is
a
hyperbolic property. As usual, we will take advantage of this to simplify our
diagrams, usually by moving A to the centre of the disk.
We shall consider regions bounded by segments of i-lines. We observe that
we can add the boundary points in D to a convex region to get a larger convex
set. We shall often consider this larger set.
First, some results which are true in both euclidean and hyperbolic geometry.
Lemma 1
If S and T are convex, then so is SnT.
proof
If A and B are in SnT, then they are in S so the segment AB is in S.
Similarly, segment AB is in T, and hence it is in SnT.
Lemma 2
If S is the interior of a circle K, then S is convex.
proof
If A and B are in S, then the line L = AB cuts K exactly twice.
Then the segment AB is the intersection of L and S.
Lemma 3
If L is a line, then each side of L is convex.
proof
If A and B are on the same side of L, then the line AB cuts L at most once.
It follows that the segment cannot contain a point C on the opposite side,
since otherwise, the segments AC and CB would each cut L.
We do require one result which is easiest to state for hyperbolic geometry alone.
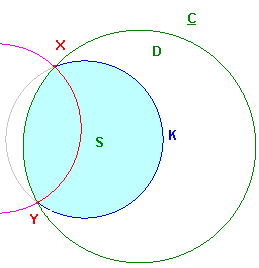
If a circle K meets the boundary C at X and Y, then
(a) K divides D into two regions, S and T,
(b) the hyperbolic line XY lies entirely in one, S, say,
(c) S is convex.
The figure on the right shows one possible case. The boundary is called
a hypercircle
Finally, we consider the case of a horocycle.
Lemma 5
If S is the interior of a horocycle K, then S is convex.
The proof is similar to that of Lemma 4. We leave it as an exercise.
cuts B only in the points U and V. By convexity, the segment UV is in S.
By Lemma 3, each side of L is convex. By Lemma 1, the intersection of
each with S is again convex, and each has the segment as part of its
boundary. We may proceed in this fashion and obtain a convex region
whose boundary consists of segments.
If we begin with a circle (Lemma 2), and always choose points on the
remaining circular arc, we get a convex cyclic polygon.
If we use a figure like that in Lemma 4, choose XY as our first
segment,
and pick the region not including the arc of C, we get a convex polygon
whose vertices lie on an arc of an i-line which is not a hyperbolic line.
To avoid the inclusion of X and Y - which are not in the hyperbolic plane -
we could begin with a segment joining two points of the blue arc. Such a
figure may be called a
hypercyclic polygon
From a horocycle, we similarly obtain horocyclic polygons.
definition
Suppose that B is a simple closed curve.
Then two points on B will divide
the curve into
two "arcs". We say that points A(1),...,A(n) lie in order on
the curve if for each i, the remaining points lie on the same arc A(i)A(i+1),
and A(2),...,A(n-1) lie on the same arc A(n)A(1).
As we shall usually deal with curves consisting of segments of i-lines, it is
probably easier to think of a bijection from the circle to B. If we start at
the point corresponding to A(1)
we pass the points A(2),..,A(n) in this order.
or in the order A(n),A(n-1),..,A(2).
The process of obtaining convex polygons outlined above may now be
described as choosing vertices in order on a boundary consisting of
arcs of euclidean circles, and looking at the intersections of the half-
planes which contain the other vertices.
We now look at the problem of the existance of convex polygons with
sides of prescibed length.