


|  |
The Interior Exterior Theorem
|
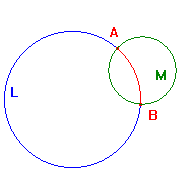
Suppose that L is an i-line. If L is an extended line, then it divides the rest of E+ into two regions, known as the sides of L. If L is a circle, then it also dvides the rest of E+ into two regions, known as the interior , the region containing the centre, and the exterior the region containing ∞. For the sake of uniformity, we shall also refer to these as sides of the circle.
We know that an inversive transformation t maps L to an i-line,
The concept of region is essentially topological, but we wish to give a
|
|
|
The Interior-Exterior Theorem. If L is an i-line and tεI(2), then t maps the sides of L to the sides of t(L).
A nice way to show this would be to prove that if two points A and B lie
|
|
|
In euclidean geometry, the idea of a segment is best described using the idea of betweenness. However, we cannot say that, for three points on an circle, one lies between the other two in any meaningful way.
The Interior-Exterior Theorem does allow us to define segments of i-lines
Definition
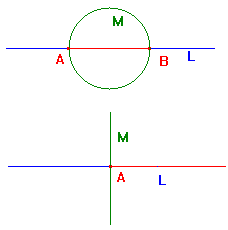
The existence and uniqueness of such an M is guaranteed by
It might appear simpler to take any i-line M through A and B, but then
If L is a circle, this produces the obvious result - the euclidean arcs of L. |
|
| After the Interior-Exterior Theorem, it is easy to see that inversive transformations map i-segements to i-segements. We have
The i-segment Theorem |
| Main inversive page |