Main work

• Convection and magnetic field generation in rotating spherical fluid shells.
  
  Stellar and planetary magnetic fields, including the best known geomagnetic field, are among the most notable properties of stars and planets and play a crucial part in a variety of cosmic processes. The established theory of the nature of these magnetic fields field is that they are generated by a dynamo process driven by convection in the fluid regions of planets and stars. These regions are inaccessible for direct observations, e.g. the Earth's fluid outer core where the geomagnetic field is generated is located at some 2800km below the surface of the planet. Self-consistent numerical models are thus one of the very few methods available to obtain key insights into the convection-driven dynamo process as well as into a myriad of other aspects of stellar and planetary structure and dynamics where many questions still remain open.
  
  In the last 10 years, we have developed cutting-edge numerical models and expertise in simulation of geo- and planetary magnetic fields. We solve the fully nonlinear magnetohydrodynamic equations, derived from first-principles without ad-hoc turbulent and transport models. Although restricted to moderately turbulent regimes by the computing power available at present, this approach is desirable for its self-consistency. By studying the parameter dependences and the basic physical mechanisms of the convection and the dynamo processes, we hope to achieve a meaningful extrapolation towards the turbulent regimes of actual stellar and planetary magnetic fields.
  
  While the state-of-the-art models still fall short of resolving the full details of the geo-, planetary and stellar magnetic fields, it is essential to keep building up capability in this area. For instance, the presence of the geomagnetic field has broad implications for life on our planet. It shields Earth's surface from harmful incoming radiation and protects the many man-made satellites orbiting the planet. Geomagnetism has been long used as a navigational aid by humans and animals and has fascinated people since antiquity. Similarly important are the studies of solar magnetism, which is so strong that it controls much of the visible solar activity, and of planetary magnetism, which can tell us much about the geology and the formation of planets.
  
  For additional details on the subject in general and on my work in particular visit my list of publications.
  
  
  

• Excitation and propagation of waves in cardiac tissue and other excitable media.
  
  
  
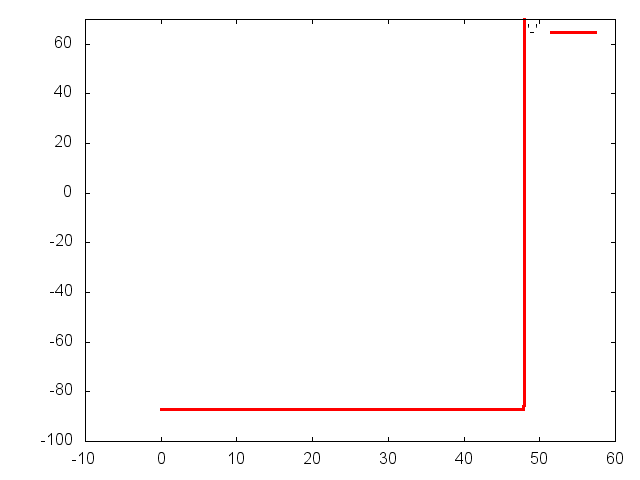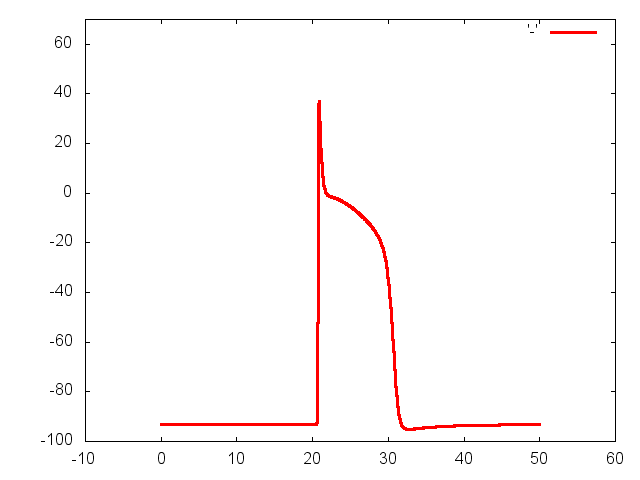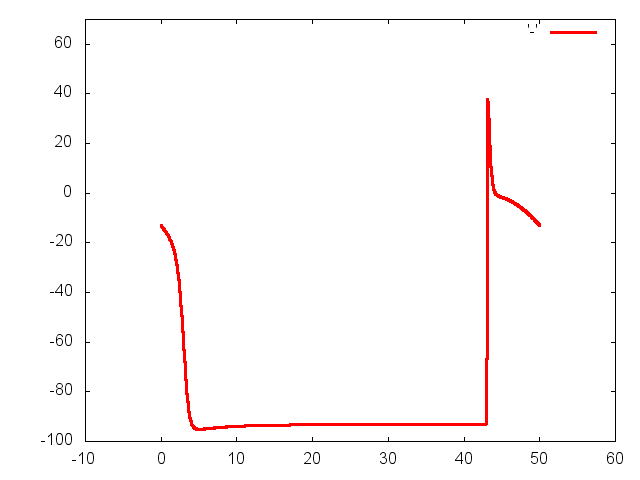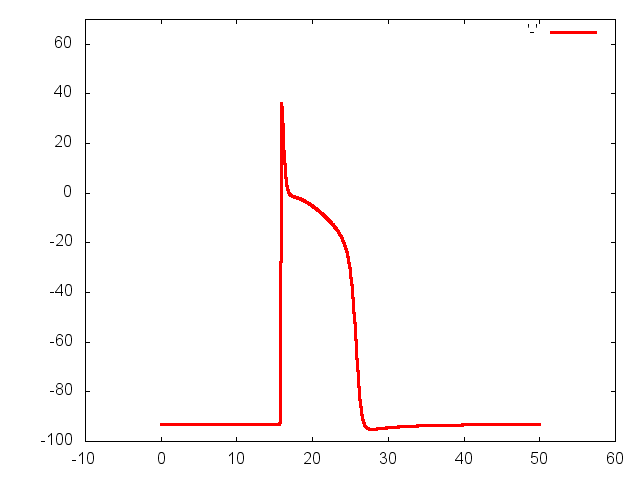
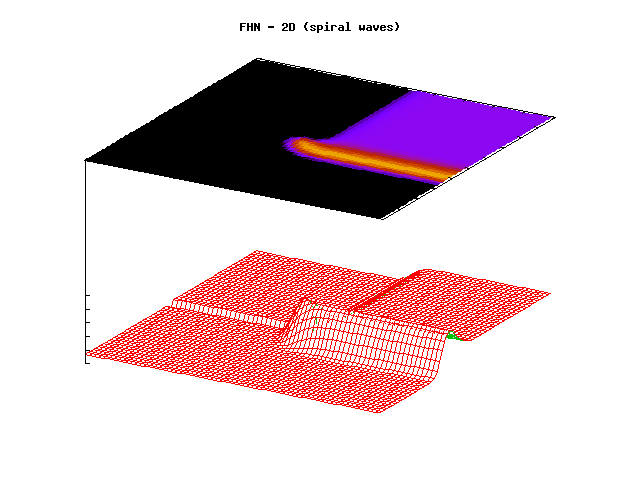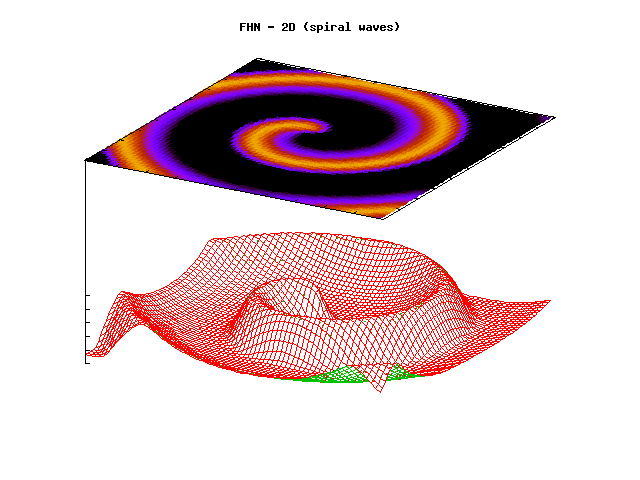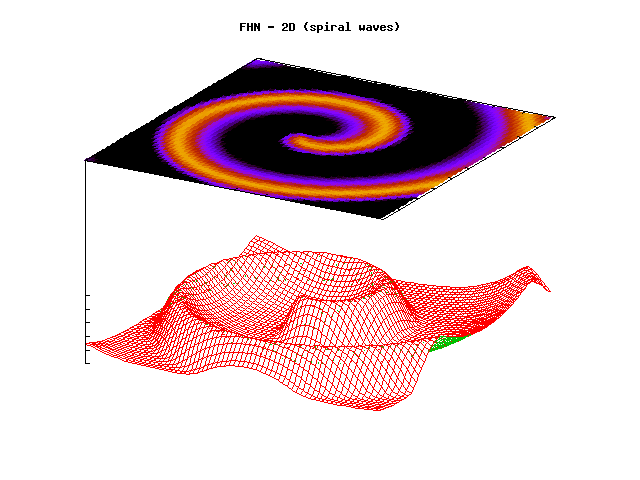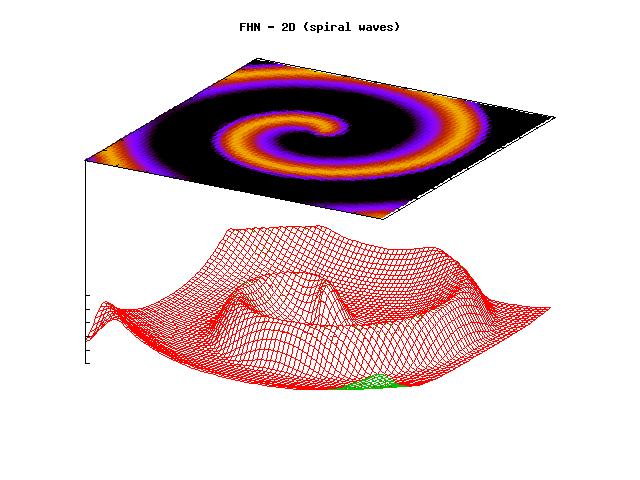
  Through coordinated contraction of the heart, blood is pumped to all parts of the human body ensuring our health and vitality. This mechanical activity of the heart is controlled by electrical impulses, called action potentials, which propagate along the membranes of the cardiac cells. An irregular action potential propagation leads to irregular mechanical activity of the heart. Such conditions are known as cardiac arrhythmias. Cardiac arrhythmias are abnormal often life-threatening events. Some of them can lead to sudden cardiac death which is the leading cause of death in the industrialised world. Mathematically, the normal as well as the abnormal propagation of cardiac action potentials can be modelled by a system of partial differential equations. Thise equations are proposed on the basis of physiological measurements and differ for the various types of cardiac tissues. The contemporary cardiac models are remarkably detailed and provide impressive accuracy. They are very complicated and consist of a large number of equation and thus by necessity they have to be solved numerically. However, simplifications of the detailed cardiac models exist. Such simplifications can be achieved by taking into account the asymptotic structure of the detailed models.
  
  Click for a more mathematical description..
  
  For additional details on the subject in general and on my work in particular visit my list of publications.

General interests

• Non-linear Dynamical Systems. Non-linear partial differential equations are central to mathematics, pure and applied. They provide an universal approach to describing almost any physical system which depends on continuously varying independent variables. Their relevance is growing, powered by modern computational equipment, capable of solving suitably discretized approximations of the equations. Equally important is the impact the non-linear partial differential equations have on fundamental mathematics, opening new branches, cross-fertilising existing ones, benefiting from the results. In addition to numerical methods, I am also interested in algebraic, topological, and group methods in the theory of dynamical systems.

• Applications of Differential Equations to Physical Systems. Perturbation methods; Instability of fluid flow and in magnetohydrodynamics; Pattern formation out of statistical equilibrium; Rotating thermal convection; Dynamo theory; Geophysical fluid dynamics; Cardiac modelling.

• Recreational & Technical. Algorithms; Programming techniques, languages and tools; Computer Algebra Systems; Visualization.