Conics - the classical definition

Conics were studied by the geometers of the Greek school around the time of Euclid.
Menaechus is usually credited with their discovery.
The names ellipse, parabola and hyperbola were introduced by Apollonius.

In the nineteenth century, the ideas of projective geometry and duality were developed by
Poncelet and Gergonne.

In these pages, we shall concentrate on incidence properties
and the fundamental notion of duality.

We shall approach the subject by geometry and by algebra.

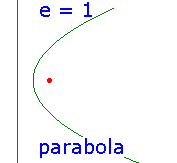
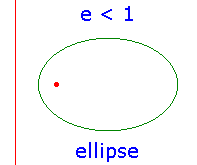
Classically, a conic C is defined in terms of
a point F, the focus,
a line D, the directrix, and
a positive number e, the eccentricity.
Then C is the locus {P : |PF|=e|PD|},
where |PD| denotes the distance of the point P from the line D.

There are three basic types of conic, depending on the value of e.
Note that e determines the shape of the conic,
the choice of the distance from F to D merely scales the picture.

Observe that each conic has an axis of symmetry through F, perpendicular to D,
this is the axis of the conic.

Conics may also be defined as sections of a cone.

Main Conics Page

Main Cabri Page