If P and Q are distinct p-points in the interior of a p-conic C, then
there are precisely two projective transformations t which satisfy
(a) t(C) = C, and
(b) t interchanges P and Q.
and each such transformation has order 2
proof
As in the proof of the two point theorem, we associate with P the
By La Hire's Theorem since RS and R'S' are the polars of p-points on AB,
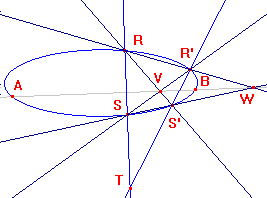
Let RR' and SS' meet in W, and RS', R'S meet in V.
But AB is the polar of T, so, by (1), V,W lie on AB.
By the Corollary to the cross-ratio theorem,
Now suppose that t satisfies (a) and (b).
Since it interchanges A and B, it fixes AB, and hence fixes T, the pole of AB.
We know that t maps R to one of R' and S', and S to the other.
Suppose that t maps R to R', and hence S to S'.
The case where t(R) = S' is very similar (using V rather than W).
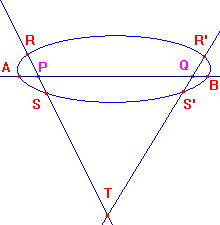
Let the p-line PQ meet C in A,B, and let T be the pole of AB.
chord RS through P, the polar of the intersection of AB with the polar of P.
Likewise, we associate with Q, the chord R'S' through Q.
they meet in T (the pole of AB).
By the inscribed quadrilateral theorem , we have
(1) VW is the polar of T, and
(2) TV is the polar of W.
Also, by (2), V is the intersection of AB and the polar of W.
one of V,W lies inside C, and one outside.
As in the proof of the two point theorem,
and that of the interchange theorem, we see that
t interchanges A and B, and also {R,S} and {R',S'},
since it interchanges P and Q.
Since it maps {R,R',S,S'} to itself, it must also fix the set {V,W} - as the
other intersections of pairs of these p-points. But t maps C to itself, so
by the interior-exterior theorem, t must fix V and W since only
one
of V,W is inside C.
Also, t fixes W, so it maps RW to R'W.
It must therefore map R' to the other intersection of R'W and C, i.e. R.
Similarly, it must map S' to S.
Thus t2 fixes R,R',S,S'. Since these four p-points are on the p-conic C,
the three point theorem allows us to conclude that t2 is the identity.